Matrices explained - Part 1

October 04, 2020

Introduction

This series of blog posts is going to cover how transformation matrices work and how to leverage them to take precise control over your rigs most of this is going to be through the lens of a Maya Rigger but the knowledge is applicable in pretty much any 3D app.

Matrices are at the core of any 3D application and understanding how they store transformations as well as how they interact with each other is going to give you a much deeper understanding of what actually goes on when you move or constrain stuff around.

Quick disclaimer before we jump in, All my knowledge about matrices is self taught. I have built a good intuition of how they work and how the operations you can do on them behave but I don't actually know how the math works under the hood.

But enough rambling around, let's jump in.

So, what is a matrix?

In the context of a 3D application, a matrix is simply a representation of a transformation. One transformation matrix can encode the translation, orientation, scale and shearing of an object. Transformation matrices are stored as 4x4 matrices, meaning they have 4 rows and 4 columns and they look like this:

$Identity= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

What you're seeing here is is called the Identity matrix, it's filled with zeros and have ones on the top left to bottom right diagonal.

Maya uses row major matrices, meaning the data it stores are encoded into its rows. You might see column major matrices if you use other applications (including Maya's Bifrost, Blender and more). But let's stick with row major for now as this is what I'm mostly used to working with.

The last column of the matrix is only there for us to have a square matrix but doesn't actually do anything, just remember that it's 0, 0, 0, 1 and you're good. I am not 100% sure of that last part but this assumption hasn't caused me any trouble so far.

Edit: That last column can be used to represent the camera projection in 3D engines, definitely not something you need to worry about unless you're writing your own engine so let's continue with that assumption that it's just 0, 0, 0, 1 and we'll be just fine.
Thanks Willem for the info.

Translation

The easiest part of a matrix to explain is the translation. Your translate X/Y/Z values are simply thrown in the last row.
For example the matrix that stores the translation of (3, 4, 2) looks like this:

$Translation= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 3 & 4 & 2 & 1 \\ \end{bmatrix}$

And that's pretty much it for translations, just remember stick a 1 in the last column and leave it at that.

Orientation, Scale and Shear

You might be wondering why the Translation had its own section but the Orientation, Scale and Shear are grouped together. That's because all three are represented in the same place inside the matrix.

How is that possible you ask?

Well they aren't stored as is but are rather the interpretation of something else: 3 Vectors. You know them already, it's those three fellas:

Identity Matrix Representation

Let's copy the identity matrix here again and break it down a bit

$Identity= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

Ignoring the last column, let's have a look at the first three rows:

First row is the X vector of our object and looks like this: (1, 0, 0) This means our X vector points one unit out in the world X and 0 in Y/Z
Second row is the Y vector: (0, 1, 0) Our Y vector points one unit in world Y and 0 in X/Z
Third row: (0, 0, 1) Our Z vector points one unit in world Z and 0 in X/Y

Since this is the identity matrix, all the vectors line up with the world's, makes sense.

The rest of this post going to explain what happens when we change those 3 rows so make sure you have a grasp of what we just said. If you're struggling, keep going, the scale and orientation sections will likely help you wrap your mind around the idea more.

Scale

Scaling a matrix is simply a matter of scaling those vectors. By default they are unit vectors, meaning they have a length of one but let's change that.

In this example we're scaling our matrix by 2 on the X axis, meaning our X vector gets a length of 2 while the other two don't change.

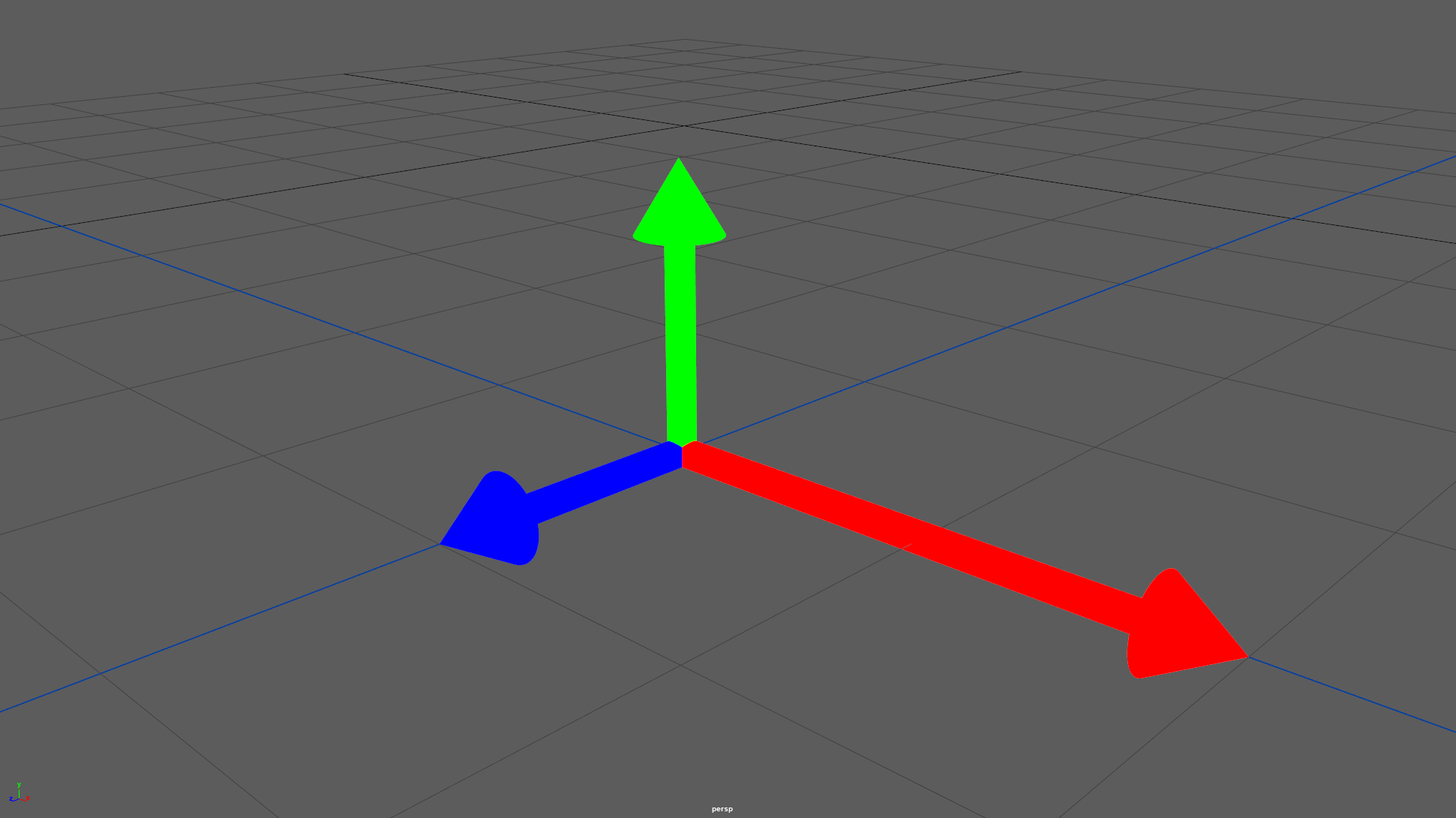
X axis scale

$scaleX= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

And here's an example of a negative scale along the Z Axis:

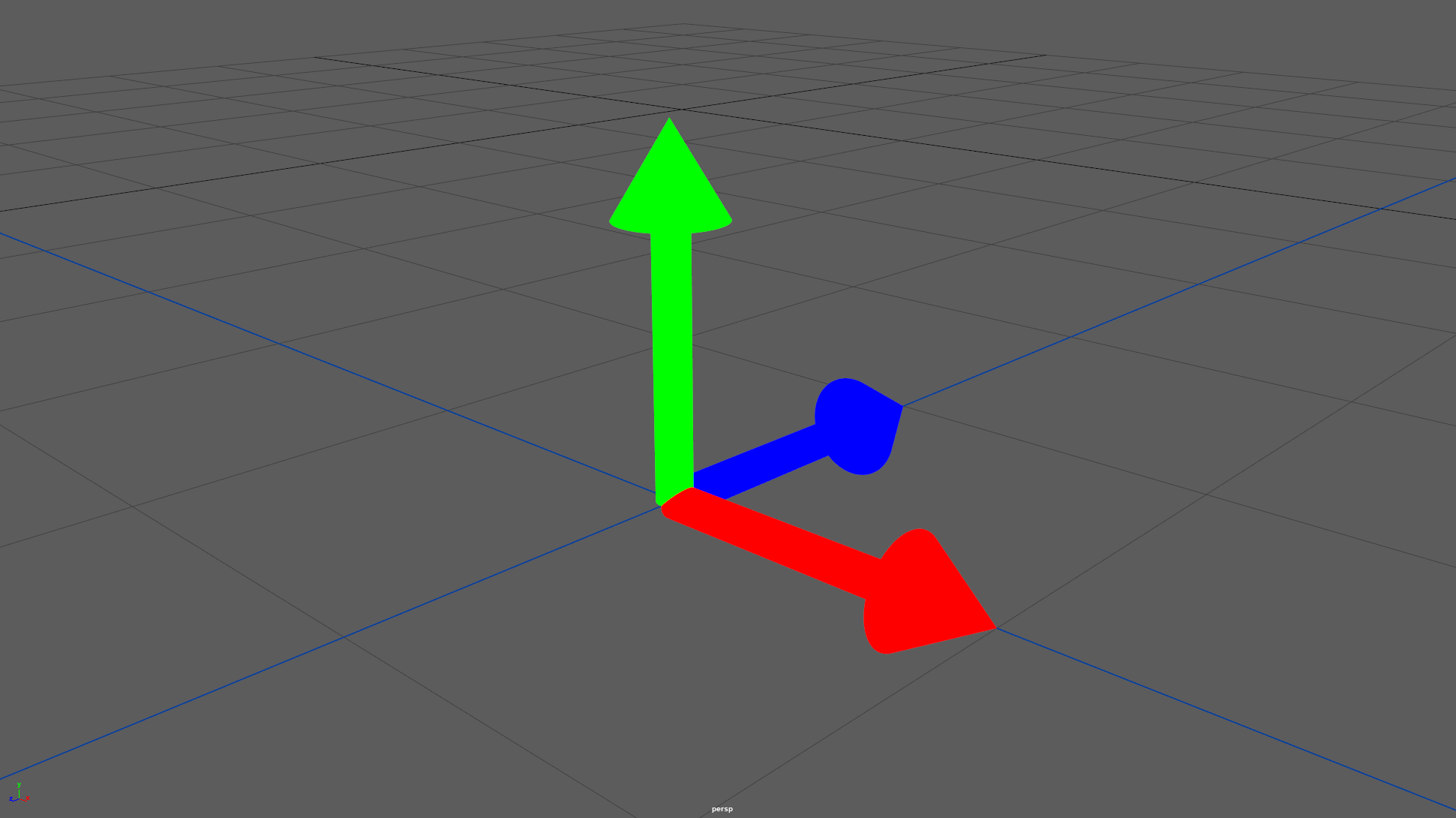
Negative Scale on Z

$ScaleZ (negative)= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

Here the length of all our vectors is still 1 but the Z vectors has flipped its direction.

Orientation

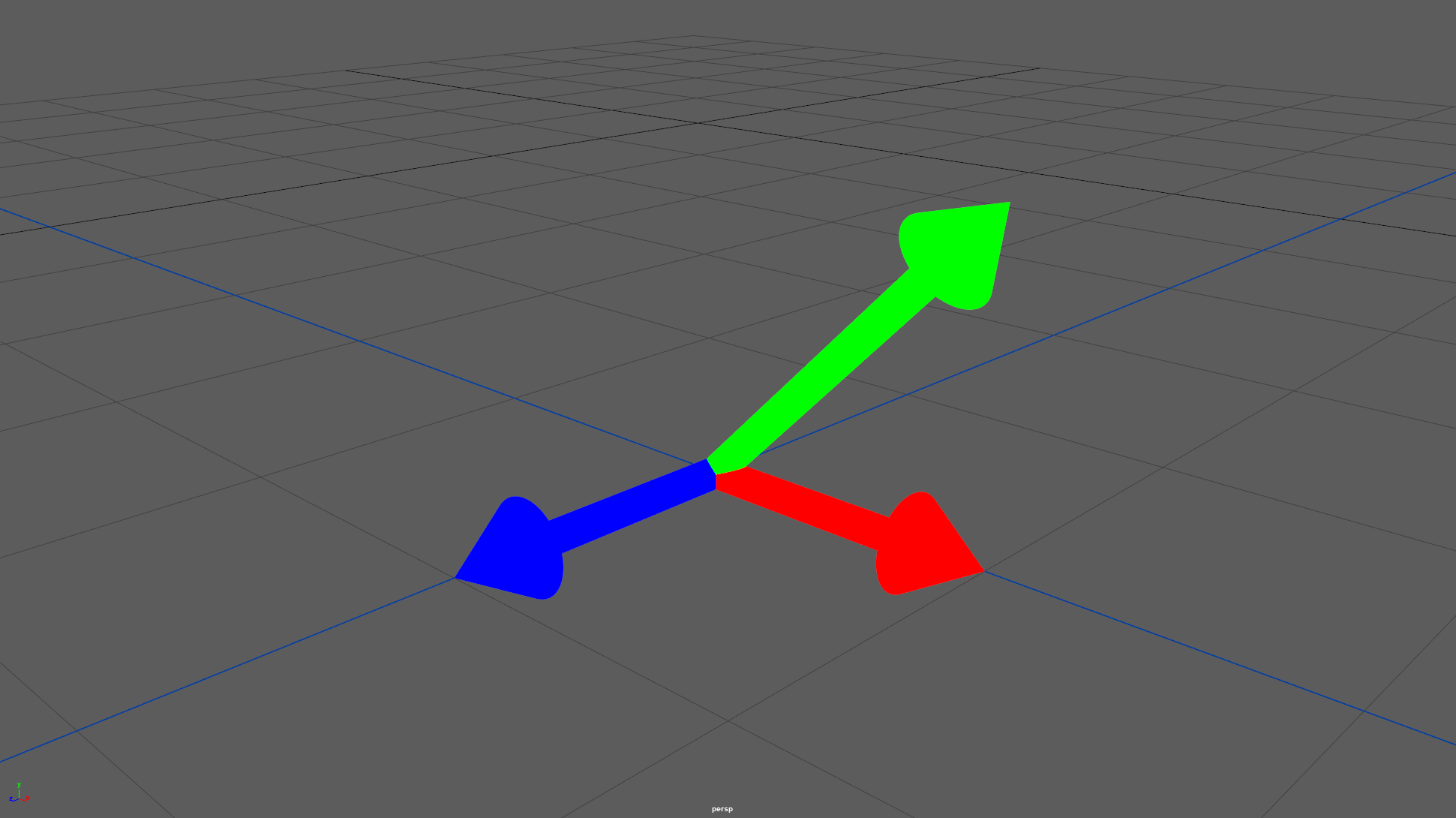
Up until now we've kept our vectors on the same line as the world vectors, let's spice it up a bit and make a 90° rotation around the Z axis

Here's a screenshot of the result, see if you can predict what the matrix looks like from that (you can see the world vectors in the lower left corner of the screenshot to help you):

90° rotation on the Z axis

Here's the answer:

$RotateZ= \begin{bmatrix} 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

If you didn't find that, no problem, let's break it down a bit like we did with the identity matrix.

First row (X): $(0, 1, 0)$
The X vector now points towards world Y.
Second row (Y): $(-1, 0, 0)$
The Y vector now points 1 unit towards the world's -X.
Third row (Z): $(0, 0 , 1)$
The Z vector hasn't changed since the rotation happened around it.

Shearing

Small disclaimer, this is the part of matrices I've used the least and therefore am the least comfortable with so take this with a grain of salt. Generally if I get shearing it means I messed up my math somewhere ¯\_(ツ)_/¯

Up until now, our three XYZ vectors were all orthogonal to each other. Introducing shearing breaks this.

Let's take a quick example of that where our Y vector points towards both Y and X

Shearing on the Y axis

$Shear= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

By now you should be able to make sense of this matrix but I'll go over it anyway. Nothing has changed except our Y vector (2nd row), it now goes 1 unit in world Y and 1 unit in X, resulting in the vector not being orthogonal to the X vector anymore.

Conclusion

I tried to be as exhaustive as I could be if you need to remember one thing from this is this:

The translation is stored as is in the last row
The First three rows represent the X, Y and Z vectors of your object

I purposefully kept the transformations simple to keep the vectors lined up with the world as this makes for easy to read matrices but you are obviously not limited to this. You will very rarely manipulate those values directly but rather do a bit of vector math to compute your XYZ vectors and throw those in the matrix instead.

I highly recommend that you experiment with matrices yourself to build that intuition as this is going to beat any explanation in your understanding of them. Maya 2020's offset parent matrix is great for that because you can manipulate the matrix directly in the attribute editor:

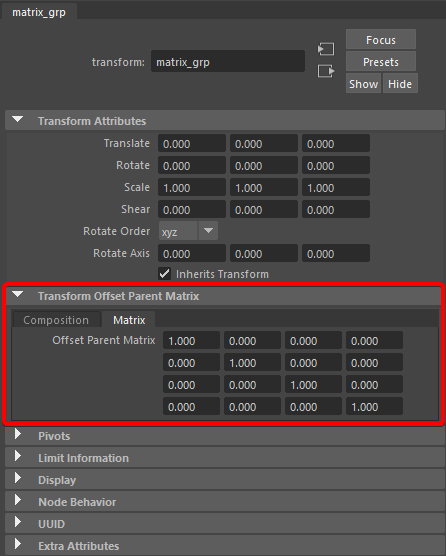
Offset Parent Matrix UI

The "Composition" tab gives you a more traditional Translate/Rotate/Scale/Shear interface over the same matrix which is great to understand the relation between those values and the underlying matrix.

If you're looking for a cheat sheet of what we covered, Marin Petrov has a great Zine that does this and more

Time for another Zine for TDs. This one is about Transformation Matrices (mostly in Maya) 😃#cg #animation #math #LinearAlgebra pic.twitter.com/scEHrbBo7K
— Marin Petrov 🇺🇦 (@marinwaves) July 31, 2020

The next post is going to cover how to apply transformations through matrix multiplications.

Back to top